Happy Numbers

Image from Wikipedia

Intro

An integer is happy if, when calculating the sum of the squares of its digits, then the sum of the squares of the digits of the resulting number, and so on, it eventually reaches 1. Otherwise, the number is unhappy.

This give me the opportunity to “play” with 2 different code in Python and check which one is faster. I then compare timings with a C++ implementation.

At the end you should be able to solve your first puzzle on CodinGame. If you never did before, make a try. This is really fun.

First Python Code

Let’s check if 24 is happy. Here is the code :

def sum_of_squared_digits2(n1:int)->int:
    n2 = 0
    while n1:
        digit=n1%10
        # n2 += pow(digit, 2)
        # n2+=digit**2
        n2+=digit*digit
        n1=n1//10
    n1=n2
    return n2


n_set = set()
n = 24

while (n!=1 and n not in n_set):
    n_set.add(n)
    n = sum_of_squared_digits2(n)
    print(n)
print("Happy") if n==1 else print("Unhappy") 

This output looks like :

20
4
16
37
58
89
145
42
20
Unhappy

As you can read in the comments, I did some tests with pow() and **2 but finally using the cached value digit was more efficient.

Second implementation

Here I try to simplify sum_of_squared_digits()

• The one liner goes like this :
  • Convert n in a string
  • Then read each “char” (digit) of the string
  • Convert each char as an int
  • Elevate the int to power of 2

def sum_of_squared_digits(n:int)->int:
    return sum([int(i)**2 for i in str(n)])

n_set = set()
n = 24
while (n!=1 and n not in n_set):
    n_set.add(n)
    n = sum_of_squared_digits(n)
    print(n)

print("Happy") if n==1 else print("Unhappy") 

No surprise, we get the same output.

However we may want to know which approach is faster. One thing I learned with optimized C++ compiler:

• When it comes to benchmarks, never assume. Measure!

Benchmarking 1 in Python

import time

k_MAX=100_000

def sum_of_squared_digits(n:int)->int:
    return sum([int(i)**2 for i in str(n)])

start_time = time.time()  # Start timer

for n in range(1, k_MAX+1):
    n_set = set()
    n_init = n
    while (n!=1 and n not in n_set):
        n_set.add(n)
        n = sum_of_squared_digits(n)

end_time = time.time()  
print(f"Execution time: {end_time - start_time:.6f} seconds")

Execution time: 0.797350 seconds

Benchmarking 2 in Python

import time

k_MAX = 100_000

def sum_of_squared_digits2(n_in:int)->int:
    n_out = 0
    while n_in:
        digit=n_in%10
        n_out += digit*digit
        n_in=n_in//10
    n_in=n_out
    return n_out

start_time = time.time()  # Start timer

for n in range(1, k_MAX + 1):
    n_set = set()
    n_init = n
    while n != 1 and n not in n_set:
        n_set.add(n)
        n = sum_of_squared_digits2(n)

end_time = time.time()  
print(f"Execution time: {end_time - start_time:.6f} seconds")

Execution time: 0.482066 seconds. The code of sum_of_squared_digits2() is longer but there is no string conversion etc. And we use digit which should be in the local cache of the processor. This explains the 1.6 speed ratio.

I did some testings calling the script with -O within a console but I did’nt get any significant improvement. No, I did’nt transpile Python to C.

Benchmarking in C++

• If you don’t have a C++ compiler on your host (shame on you! 😁) you can copy, past and run the code below with an online C++ compiler.
• I selected C++23 and -02 optimizations and did some test with C++20 and no optimization.

#include <iostream>
#include <unordered_set>
#include <chrono>

constexpr int k_MAX = 100'000;

int sum_of_squared_digits3(int n_in) {
    int n_out = 0;
    while (n_in != 0) {
        int digit = n_in % 10;
        n_out += digit * digit;
        n_in /= 10;
    }
    return n_out;
}

int main() {
    auto start_time = std::chrono::high_resolution_clock::now();

    for (int n = 1; n <= k_MAX; ++n) {
        std::unordered_set<int> n_set;
        int n_current = n;

        while (n_current != 1 && !n_set.contains(n_current)) {
            n_set.insert(n_current);
            n_current = sum_of_squared_digits3(n_current);
        }
    }

    auto end_time = std::chrono::high_resolution_clock::now();
    std::chrono::duration<double> elapsed_seconds = end_time - start_time;
    std::cout << "Execution time: " << elapsed_seconds.count() << " seconds\n";
    return 0;
}

Execution time: 0.083385 seconds

• For such a simple algorithm, the syntax is very similar across languages. So, even if Python is the only programming language you know, you should understand what is happening here. Additionally, I kept the variable names the same.
• 34 lines in C++ vs 24 in Python
• 0.08 sec in C++ vs 0.48 sec in Python
• 6 times faster

Benchmarking C++ V2

#include <iostream>
#include <unordered_set>
#include <array>
#include <chrono>

constexpr int k_MAX = 100'000;

constexpr std::array<int, 10> k_squares = [] {
    std::array<int, 10> squares{};
    for (int i = 0; i < 10; ++i) {
        squares[i] = i * i;
    }
    return squares;
}();

int sum_of_squared_digits2(int n_in) {
    int n_out = 0;
    while (n_in != 0) {
        int digit = n_in % 10;
        n_out += k_squares[digit];
        n_in /= 10;
    }
    return n_out;
}


int main() {
    auto start_time = std::chrono::high_resolution_clock::now();

    for (int n = 1; n <= k_MAX; ++n) {
        std::unordered_set<int> n_set;
        int n_current = n;

        while (n_current != 1 && !n_set.contains(n_current)) {
            n_set.insert(n_current);
            n_current = sum_of_squared_digits2(n_current);
        }
    }

    auto end_time = std::chrono::high_resolution_clock::now();
    std::chrono::duration<double> elapsed_seconds = end_time - start_time;
    std::cout << "Execution time: " << elapsed_seconds.count() << " seconds\n";
    return 0;
}

The timing is similar.

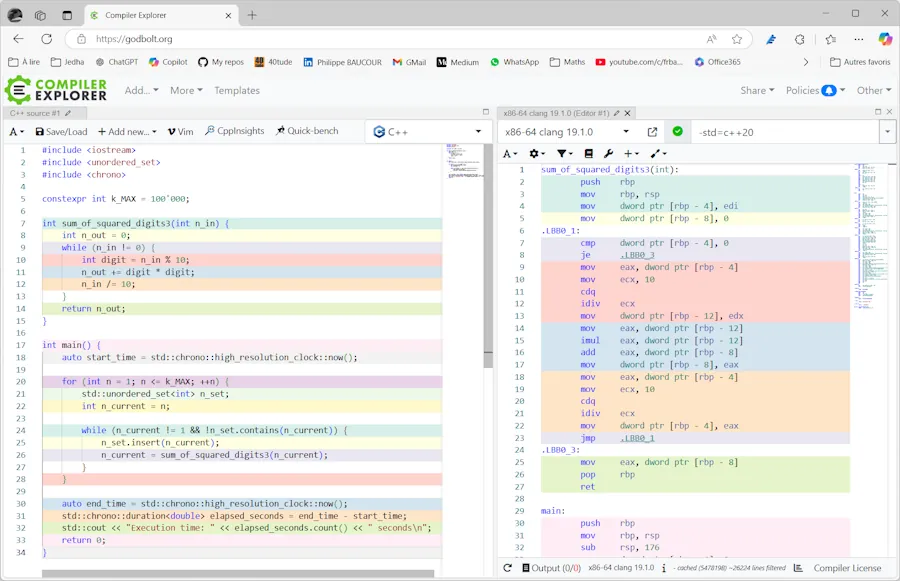
I suspect the optimizer is doing a great job. I did’nt look at assembly language but you can use Compiler Explorer to do so. It is always very interesting. Read this article to see a real case where looking to assembly language was THE solution.

Again, even on Compiler Explorer, make sure to select C++ 20 or later otherwise the n_set.contains(n_current) function call is not be available.

Conclusion

• Yes, we could have used numpy and see what happen when vectorizing the algorithm.
• Yes, we could do a better job with some multithreading etc.
• But… It is always a tradeoff between the time spent vs speed improvement
• Regarding speed improvement vs time spent, feel free to read this post about Sieve of Eratosthenes
• Now you should be able to solve this puzzle on CodinGame

PS :

Try this

import time
from functools import lru_cache

k_MAX = 100_000

@lru_cache(maxsize=None)
def sum_of_squared_digits2(n_in: int) -> int:
    n_out = 0
    while n_in:
        digit = n_in % 10
        n_out += digit * digit
        n_in = n_in // 10
    return n_out


start_time = time.time()  

for n in range(1, k_MAX + 1):
    n_set = set()
    n_init = n
    while n != 1 and n not in n_set:
        n_set.add(n)
        n = sum_of_squared_digits2(n)

end_time = time.time()
print(f"Execution time: {end_time - start_time:.6f} seconds")

Execution time: 0.287076 seconds