La forme canonique

Introduction
C’est moyennement intéressant car cela ne concerne que les polynômes de degré 2. T’as vu, ça donne vraiment envie de lire la suite…
On veut écrire \(f(x)=ax^2+bx+c\) sous la forme \(aX^2+ \beta\) soit encore \(a(x-\alpha)^2 + \beta\)
La dernière forme, c’est la forme canonique.
Heu… Pourquoi? J’veux dire, pourquoi tu veux me prendre la tête avec la forme canonique d’un pauv’ polynôme de d°2?
En fait on va en reparler à la fin mais ce que tu dois retenir ici c’est que si j’ai la forme canonique du polynôme alors je sais :
- Comment la courbe est orientée (branches en l’air ou en bas)
- À quelle valeur de \(x\) se trouve son maximum (respectivement son minimum)
- À quelle hauteur (\(y\)) se trouve l’extremum en question
Bref, l’expression canonique (sous réserve qu’elle soit pas trop prise de tête à déterminer) permet, sans graphique, de savoir à quoi ressemble la courbe.
Calcul de \(\alpha\) et \(\beta\)
On commence en posant l’égalité
\[\begin{align*} ax^2+bx+c & = a(x-\alpha)^2 + \beta \\ ax^2+bx+c & = a (x^2 - 2 x \alpha + \alpha^2) + \beta \\ ax^2+bx+c & = ax^2 - 2ax\alpha + a \alpha^2 + \beta \end{align*}\]Ça doit passer crème. À la seconde ligne on développe et à la troisième on fait le ménage.
Maintenant, on égalise membre à membre. En français dans le texte cela veut dire que les facteurs de \(x^2\) sont égaux entre eux, idem pour les facteurs de \(x\) ainsi que les constantes. On se retrouve avec 3 égalités :
\[\begin{align*} a & = a \\ b & = -2a\alpha \\ c & = a \alpha^2 + \beta \end{align*}\]De la seconde égalité on tire :
\[\alpha = - \frac{b}{2a}\]Ca, ça doit te rappeler quelque chose. C’est la valeur de la racine quand elle est unique. C’est surtout le milieu des 2 racines. Enfin bref, ça doit te dire quelque chose.
Avec la troisième égalité on obtient :
\[\beta = c - a \alpha^2\]Or, on vient de trouver que :
\[\alpha = - \frac{b}{2a}\]Donc on peut écrire :
\[\begin{align*} \beta & = c - a \alpha^2 \\ \beta & = c - a (- \frac{b}{2a})^2 \\ \beta & = c - a \frac{b^2}{4a^2} \\ \beta & = c - \frac{b^2}{4a} \\ \beta & = \frac{4ac}{4a} - \frac{b^2}{4a} \\ \beta & = \frac{4ac - b^2}{4a} \\ \beta & = -\frac{b^2 - 4ac}{4a} \\ \beta & = -\frac{\Delta}{4a} \end{align*}\]Mouai…Ça fait pas encore rêver cette histoire. Cela dit, à ce stade on peut quand même dire que :
\[ax^2+bx+c = a(x-\alpha^2) + \beta\]Avec
\[\alpha = - \frac{b}{2a}\]Et
\[\beta = -\frac{\Delta}{4a}\]Calculons f(\(\alpha\))
\[f(x)=ax^2+bx+c\]Donc
\[f(\alpha)=a\alpha^2+b\alpha+c\]Or
\[\alpha = - \frac{b}{2a}\]On a donc :
\[\begin{align*} f(\alpha) & = a(- \frac{b}{2a})^2 + b(- \frac{b}{2a}) + c \\ f(\alpha) & = a(\frac{b^2}{4a^2}) - (\frac{b^2}{2a}) + c \\ f(\alpha) & = \frac{b^2}{4a} - \frac{2b^2}{4a} + c \\ f(\alpha) & = \frac{b^2}{4a} - \frac{2b^2}{4a} + \frac{4ac}{4a} \\ f(\alpha) & = \frac{b^2 - 2b^2 + 4ac}{4a} \\ f(\alpha) & = \frac{- b^2 + 4ac}{4a} \\ f(\alpha) & = - \frac{b^2 - 4ac}{4a} \\ f(\alpha) & = - \frac{\Delta}{4a} \\ \end{align*}\]Donc \(\beta = f(\alpha)\)
Dorénavant on peut dire :
\[ax^2+bx+c = a(x-\alpha)^2 + \beta\]Avec
\[\alpha = - \frac{b}{2a}\]Et
\[\beta = f(\alpha)\]Ça c’est plutôt cool. Watch this!
Mise en pratique pour montrer que c’est facile et utile
On se donne \(f(x) = 2x^2 -12x + 22\)
Exprimez \(f(x)\) sous sa forme canonique
Fastoche! On commence avec \(\alpha\)
\[\alpha = - \frac{b}{2a} = - \frac{-12}{4} = 3\]Ensuite on trouve \(\beta\)
\[\beta = f(\alpha) = 2\alpha^2 -12\alpha + 22 = 2 * 3^2 - 12 * 3 + 22 = 18 - 36 + 22 = 4\]Donc sous sa forme canonique on a :
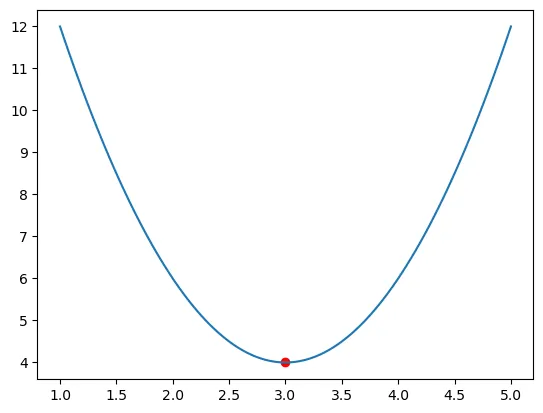
\[\begin{align*} f(x) & = a(x-\alpha)^2 + \beta \\ f(x) & = 2(x-3)^2 + 4 \end{align*}\]Une fois écrit sous cette forme on peut dire que :
- La parabole est convexe. Ses branches sont en l’air (\(a>0\))
- Son minimum arrive que \(x = \alpha = 3\)
- Que la valeur de \(f(x)\) en ce point vaut \(4\)
C’est bien ce que l’on retrouve si on trace la courbe.
# Pas la peine de lire ces lignes
# Ce qui compte c'est le graphe qui suit
def f(x) :
return 2*(x-3)**2 + 4
fig, ax = plt.subplots()
x = np.linspace (1, 5, 100)
ax.plot(x, f(x))
_ = ax.scatter(3, 4, c='red')
Une autre façon de raisonner
On veut toujours écrire \(f(x)=ax^2+bx+c\) sous la forme \(a(x-\alpha)^2 + \beta\)
Pour y arriver, on va écrire le début de \(f(x)\) comme une identité remarquable.
\[\begin{align*} f(x) & =ax^2 + bx + c \\ f(x) & =a(x^2+x \frac{b}{a}) + c \end{align*}\]Là, la ruse consiste à dire que ce qu’il y a dans la parenthèse ressemble au début d’une identité remarquable. Un truc du style :
\[( A + B)^2 = (A^2 + 2AB +B^2)\]OK… Dans la parenthèse on a :
\[x^2 + x \frac{b}{a}\]Et ça, c’est censé ressembler au début de \((A^2 + 2AB + ...)\)
Développons \((x + \frac{b}{2a})^2\). Il faut bien voir le \(2\) au dénominateur.
\[\begin{align*} (x + \frac{b}{2a})^2 & = x^2 + 2 * x * \frac{b}{2a} + (\frac{b}{2a})^2 \\ (x + \frac{b}{2a})^2 & = x^2 + x * \frac{b}{a} + (\frac{b}{2a})^2 \end{align*}\]On reconnaît, à droite de l’égalité le début de notre écriture de \(f(x)\). On avait :
\[f(x)=a(x^2+x \frac{b}{a}) + c\]Et ici on peut dire que :
\[(x + \frac{b}{2a})^2 - (\frac{b}{2a})^2 = x^2 + x * \frac{b}{a}\]Si on remplace dans l’expression de \(f(x)\) on a :
\[\begin{align*} f(x) & = a(x^2 + x \frac{b}{a}) + c \\ f(x) & = a((x + \frac{b}{2a})^2 - (\frac{b}{2a})^2) + c \\ f(x) & = a((x + \frac{b}{2a})^2 - \frac{b^2}{4a^2}) + c \\ f(x) & = a (x + \frac{b}{2a})^2 - a \frac{b^2}{4a^2} + c \\ f(x) & = a (x + \frac{b}{2a})^2 - \frac{b^2}{4a} + c \\ f(x) & = a (x + \frac{b}{2a})^2 - \frac{b^2}{4a} + \frac{4ac}{4a} \\ f(x) & = a (x + \frac{b}{2a})^2 + \frac{4ac - b^2}{4a} \\ f(x) & = a (x + \frac{b}{2a})^2 + \frac{\Delta}{4a} \end{align*}\]On retrouve bien ce que nous avions précédement :
\[ax^2+bx+c = a(x-\alpha)^2 + \beta\]Avec
\[\alpha = - \frac{b}{2a}\]Et
\[\beta = \frac{\Delta}{4a} = f(\alpha)\]À retenir
- La forme canonique \(ax^2+bx+c = aX^2+ \beta = a(x-\alpha)^2 + \beta\)
- \(\alpha = - \frac{b}{2a}\). L’abscisse de l’extremum (le centre des deux racines ou l’abscisse de la racine unique)
- \(\beta = f(\alpha)\). L’ordonnée de l’extremum